Chapitre 5 Garanties de délai
sans état par flot
5.1 Introduction du chapitre
Dans le chapitre précédent, nous avons utilisé une approche basée sur un
changement d'échelle du modèle classique de gestion par flot de la qualité
de service. Comme toutes les solutions basées sur le principe de
l'agrégation, elle entraîne intrinsèquement une perte de flexibilité
puisqu'on ne peut plus faire de gestion par flot. L'exemple le plus
évident de ce manque de flexibilité est l'impossibilité de traiter le
multicast. De même, dans le cas des flots GS nous étions obligés de fournir
le même délai à tous ou de gérer un b-flot pour chaque délai.
L'approche que nous nous proposons d'étudier dans ce chapitre est similaire
dans ses grandes lignes à celle présentée dans le chapitre 4 : des
réseaux mettant en oeuvre le modèle IntServ/RSVP sont interconnectés par
un backbone utilisant un modèle différent mais capable de fournir le
même type de garanties.
Nous proposons une méthode permettant de résoudre les problèmes de
scalabilité sans pour autant diminuer la flexibilité. Le but est de
conserver une granularité minimale dans la gestion des flots, mais en
réduisant la nécessité de maintenir des états pour chaque flot à l'intérieur
du backbone qui devient une ``zone sans état''.
Nous commençons par situer notre travail dans le cadre des garanties de
délai dures, et décrivons les différences entre les disciplines de service
weighted fair queuing et virtual clock. Puis nous décrivons
rapidement une proposition pour le plan de contrôle, c'est à dire une
méthode pour faire un contrôle d'admission par flot sans maintenir d'état
pour chaque flot. Nous discutons ensuite le plan de données et montrons que
le trafic étant contraint en entrée, on peut supprimer les états par flot et
prévoir les effets de cette suppression sur les garanties. Cependant, les
outils analytiques ne pouvant nous donner des bornes sur ces effets que dans
des cas pires, nous utilisons des simulations pour obtenir
des estimations plus réalistes.
5.2 Préliminaires
5.2.1 Gestion des garanties dures
Plusieurs types de services doivent être proposés dans un réseau à
intégration de services. Certaines applications ont besoin de garanties
dures alors que d'autres peuvent se contenter de garanties statistiques. Un
autre ``service'' hautement désirable pour le trafic best-effort est
le partage équitable de la bande passante. Tous ces services doivent pouvoir
être proposés dans l'ensemble du réseau.
Nous plaçons notre travail dans le contexte de garanties de délai ``dures'',
par exemple le service GS de l'IntServ. Nous pensons en effet que c'est le
cas le plus difficile, et celui pour lequel on a le plus besoin de
flexibilité. Pour des services du type controlled load, des solutions
comme SRP peuvent être suffisantes. Pour l'aspect partage équitable de bande
passante, des mécanismes du type RED (Random Early Detection) nous
semblent bien plus intéressants car ils peuvent fournir une équité globale
par opposition aux techniques d'ordonnancement qui ne peuvent fournir qu'une
équité locale à chaque noeud.
5.2.2 Virtual Clock et Fair Queuing
Nous avons déjà dit au chapitre 2 que Virtual Clock et
Weighted Fair Queuing avaient des caractéristiques communes du point
de vue de l'implémentation, et fournissaient les mêmes garanties de délai.
Le Weighted Fair Queuing émule la discipline de service idéale GPS.
Le Virtual Clock (VC) a lui éte pensé comme émulation du TDM
(Time Division Multiplexing), une discipline bien réelle mais
utilisable uniquement dans les réseaux à commutation de circuit. Dans
[FP95], Figueira et Pasquale proposent une autre interprétation
de la discipline VC et montrent les propriétés de délais identiques à celles
de PGPS (démonstration d'ailleurs très similaire à celle faite dans
[PG93] pour PGPS). Leur interprétation consiste à considérer que VC
émule une discipline dans laquelle chacun des flots est servi par son propre
serveur FCFS à un débit fixé. Par convention, nous appellerons TDM cette
discipline.
Un serveur GPS partage la bande passante équitablement entre tous les flots
de manière dynamique, en fonction de leurs poids fi. Pour
obtenir une garantie de débit pour un flot, il faut limiter le nombre de
flots. Chaque flot i reçoit alors un débit garanti égal à (fi / å
fj) · C, C étant la capacité du serveur. C'est à partir de cette
garantie de débit que l'on déduit des garanties de délais pour les flots
dont le trafic est contraint par un seau percé.
Dans la discipline TDM, chaque flot se voit également garanti une bande
passante égale à (fi / åfj) · C et les mêmes garanties de
délai s'appliquent dans les mêmes conditions. Dans le cas du WFQ cependant,
le débit effectivement alloué à chaque flot est au minimum égal à (fi /
åfj) · C. Dès qu'un ou plusieurs flots ne sont pas actifs,
la bande passante qui leur est allouée est immédiatement partagée
équitablement entre les autres flots, qui recoivent alors un débit plus
élevé et, en conséquence, des délais plus faibles.
Dans le cas du VC, lorsque certains flots sont inactifs le débit en surplus
est alloué aux autres flots (la discipline conserve le travail --
work conserving) mais de manière arbitraire ; il n'est donc pas
possible de garantir un accroissement du débit disponible pour un flot
donné.
Néanmoins, comme les délais maxima sont basés sur le cas où le flot dispose
du minimum garanti de bande passante, les bornes de délais sont les mêmes
pour les deux disciplines. En fait, dans le cas où l'on n'est intéressé que
par les garanties de délai, VC se révèle un meilleur choix car le calcul
réalisé pour l'estampillage des paquets est plus simple, et surtout, il ne
dépend pas de l'état des autres flots.
Dans la suite, nous appellerons donc TDM la discipline de service fluide
équivalente au GPS quand tous les flots sont actifs. En ce sens,
virtual clock est une émulation de TDM de la même façon que
weighted fair queuing est une émulation de GPS.
5.3 Plan de contrôle
Le problème du plan de contrôle se ramène à la question de comment réaliser
un contrôle d'admission sans maintenir d'état par flot. Nous ne détaillerons
pas le problème mais décrirons seulement les grands principes d'une solution
acceptable.
On conserve dans chaque noeud la somme Rsom des réservations allouées
pour tous les flots. Localement, le contrôle d'admission pour un flot i
demandant une réservation Ri teste si Rsom+Ri £ C (C étant la
capacité du lien). Si le test réussit, Rsom est mis à jour en
Rsom+Ri. Sinon, la réservation est refusée. Quand un flot se termine,
sa réservation doit être soustraite du total Rsom-=Ri.
5.3.2 CAC global
De la même façon que ce que nous avons proposée au chapitre 4,
l'ensemble de la zone sans état doit être perçu comme un seul élément par
les réseaux périphériques. L'interfaçage au niveau du contrôle d'admission
sera donc similaire. La réalisation du contrôle d'admission dans la zone
sans état sera par contre très différente. Deux approches sont possibles,
utiliser une architecture répartie ou un gestionnaire de contrôle
d'admission centralisé (broker). Dans les deux cas, il est impératif
d'assurer qu'aucun changement de route ne se produise.
Architecture répartie
Si on utilise une architecture répartie, chaque noeud gérant sa valeur de
Rsom il est alors primordial d'assurer la fiabilité de transmission des
messages, aussi bien d'ajout (message ADD) que d'effacement
(message DEL) de réservation. Il faut également gérer la ``remontée
d'un échec'', c'est à dire annuler les réservations faites en amont du noeud où le CAC échoue. Pour cela, le message ADD peut accumuler la
liste des noeuds parcourus. Un message CANCEL pourrait alors
remonter jusqu'à l'ingress en annulant la réservation. Ceci est décrit plus
formellement dans le tableau 5.1. Les notations car,
cdr et cons représentent les fonctions classiques de
manipulation de liste du langage Lisp.
| Message reçu |
Traitement |
| ADD(Ri, liste) |
si Rsom+Ri £ C |
Rsom+=Ri |
| |
envoie |
ADD(Ri,cons(noeud,liste)) ® suivant |
| |
sinon envoie |
CANCEL(Ri,cdr(liste)) ® car(liste) |
| CANCEL(Ri,liste) |
|
Rsom-=Ri |
| |
envoie |
CANCEL(Ri,cdr(liste)) ® car(liste) |
| DEL(Ri) |
|
Rsom-=Ri |
| |
envoie |
DEL(Ri) ® suivant |
Table 5.1 : Traitement des messages pour le contrôle d'admission
Comme nous l'avons dit, il faut assurer une fiabilité absolue de la
transmision de ces messages, sans quoi les valeurs Rsom stockées dans
les noeuds finiraient par diverger. Même si des procédures de contrôle et
retransmission des messages sont mises en place, on ne peut pas éviter des
pertes de paquets dans des cas extrêmes, par exemple la chute d'un lien. Il
est donc impératif de disposer d'un moyen de rétablir les valeurs des
Rsom de manière cohérente. Nous proposons de permettre aux noeuds de
mesurer la bande passante réservée (et non pas utilisée) par
observation du trafic, selon une idée proposée dans [SZ99].
Pour cela, un bit est utilisé dans l'en-tête des paquets. Au niveau des
ingresses, ce bit est mis à 1 pour un paquet de chaque flot sur un
intervalle de temps fixé T. Sur l'intervalle de temps, chaque noeud
ajoute à son compteur Rmes la valeur Ri stockée dans tout paquet
marqué (ayant le bit à 1) qu'il traite. À la fin de l'intervalle de temps,
Rmes vaudra la somme des réservations faites dans ce noeud divisée
par la longueur de l'intervalle1. Pour éviter que les variations de délai fassent qu'un
paquet soit compté dans le mauvais intervalle, on peut synchroniser tous les
noeuds (en utilisant par exemple NTP [Mil92]) et marquer les
paquets à peu prés au milieu de l'intervalle.
Architecture centralisée
Une solution centralisée consiste à utiliser un broker connaissant la
topologie du réseau et gérant la valeur Rsom pour chaque noeud. Le
contrôle d'admission n'étant plus réparti, les problèmes de fiabilité de
transmission ne se posent plus. La structure de données à maintenir ne pose
pas à priori de problème de scalabilité, sa taille ne dépendant que de la
taille de la zone sans état. La limite sera plutôt liée à la puissance de
calcul nécessaire pour traiter tous les contrôles d'admission, qui dépendra
de la dynamicité du trafic.
Le multicast
Le problème du multicast est particulier (et difficile) car la signalisation
et les états liés au routage multicast peuvent eux mêmes poser des problèmes
de scalabilité. La gestion de la qualité de service pour le multicast
dépendra fortement, et pourrait éventuellement être associée avec, la
signalisation liée au routage multicast. Cela sort du cadre de notre travail
et nous ne discuterons donc pas ce problème.
5.4 Plan de données
5.4.1 L'implémentation du WFQ/VC
Comme nous l'avons vu en 2.5 l'implémentation d'un ordonnanceur du
type weighted fair queuing ou virtual clock consiste
typiquement à maintenir une file de paquets triés selon une estampille
calculée par la formule suivante (Fik est l'estampille de Pik, le
kieme paquet du flot i) :
|
Fik = max(Aik, Fik-1) + |
|
(5.1) |
où Aik est la date d'arrivée du paquet (exprimée en temps virtuel pour
le WFQ et temps réel pour le VC), Lik sa taille et Ri la réservation
allouée au flot i.
De cette formule il apparaît que pour chaque flot on a besoin de connaître
les valeurs de Fik-1 et Ri. L'état à maintenir par flot dans chaque
noeud se réduit donc au couple (Fik-1, Ri). Nous ne prenons pas en
compte la gestion de tampons mémoire réservés au flot pour assurer un taux
de perte nul. Ceci sera justifié en 5.4.3.
Il est facile de se débarrasser de l'état Ri : celui-ci étant constant
dans l'espace (c'est à dire qu'il a la même valeur sur chacun des noeuds
du chemin), on peut le transporter simplement dans les paquets, dans un
champ d'en-tête réservé à cet effet. Si à un moment donné la réservation
associée à un flot change, il suffit de le refléter dans la valeur de Ri
codée dans les prochains paquets du flot (sous réserve que le contrôle
d'admission ait précédement accepté le changement de réservation).
Éliminer l'état Fik-1 est plus difficile ; d'une part il a une valeur
purement locale (il représente une date exprimée dans le référentiel
temporel de l'interface considérée), d'autre part il est hautement dynamique
: par définition, sa valeur est mise à jour pour chaque paquet du flot qui
traverse le noeud. Afin de voir de quelle façon et dans quelle mesure on
peut éventuellement éliminer cet état, nous allons maintenant examiner en
détail sa raison d'être.
5.4.2 Le rôle du terme Fik-1
Comme nous l'avons dit en 2.5, le besoin du terme Fik-1
tient au fait qu'en GPS le paquet Pik ne peut pas commencer son service
avant que le paquet Pik-1 n'ait terminé le sien, et permet donc
éventuellement d'augmenter l'estampille du paquet à la valeur qu'elle aurait
avec le serveur GPS.
Intuitivement, on peut dire que cela correspond à retarder2 un paquet qui arriverait ``en
avance''. Nous distinguons trois causes pour lesquelles un paquet est
susceptible d'arriver en avance :
- la source émet à un débit supérieur à sa réservation ;
- le paquet est plus court que le paquet précédent ;
- le noeud précédent a créé de la gigue.
Le premier point est évident. Le deuxième correspond au fait que le délai de
paquetisation étant proportionnel à la taille du paquet, un paquet plus
court subira des (aura des garanties de) délais plus faibles et aura donc
tendance à rattraper un paquet plus long le précédant. Pour le troisième
point, il est nécessaire d'examiner d'un peu plus près que nous ne l'avons
fait jusqu'à présent le fonctionnement de l'algorithme VC.
Annulation de la gigue
Celui-ci garantit qu'un paquet Pik ne finira pas sa transmission avec un
retard plus grand que Lmax/C par rapport au service fourni par
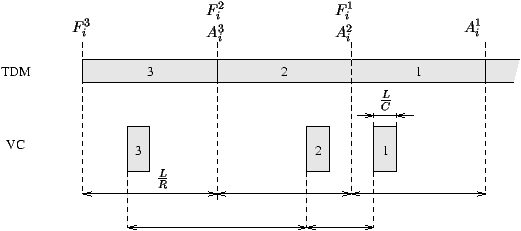
le TDM. Il peut cependant très bien le finir beaucoup plus tôt. Sur la
figure 5.1 on voit que la transmission du paquet Pik dure
Lik/Ri en TDM et Lik/C en VC, où sa transmission
peut avoir lieu (se terminer3) n'importe
où dans l'intervalle [Aik+Lik/C, Aik +
Lik/Ri + Lmax/C]. Il y a donc une incertitude égale à
Lik/Ri + Lmax/C - Lik/C sur le moment de
transmission du paquet. Pour simplifier, nous considérerons dans la suite
que l'instant de transmission du paquet est situé dans l'intervalle [0,
Lik/Ri], Aik étant égal à 0.
Figure 5.1 : Transmission des paquets en TDM et VC
Ceci implique qu'en sortie d'un noeud implémentant la politique VC,
l'espacement entre les paquets ne sera pas nécessairement (et très
probablement pas) constant et égal à L/R même si le flot était
parfaitement lissé à l'entrée dans le noeud. Au contraire, les paquets
auront tendance à ``s'agglomérer'' par paires pour former ce que nous
appellerons des ``grumeaux'' de paquets (paquets 1 et 2 sur la figure
5.1).
Dans le pire des cas, le paquet Pik-1 aura subi un délai maximum égal
à Li/Ri et le paquet Pik un délai nul. Les deux paquets se
retrouvent alors ``collés''. Notons que la simplification que nous avons
opérée sur l'intervalle d'émission possible du paquet se justifie dans la
mesure où un intervalle plus grand ne peut aggraver encore l'effet
d'agglomération (l'ordre des paquets ne peut pas être modifié).
5.4.3 Élimination du terme Fik-1
À partir de notre analyse du rôle joué par le terme Fik-1 dans
l'algorithme du VC nous pouvons maintenant envisager comment limiter les
conséquences de sa suppression. Nous avons précédement relevé trois aspects
de ce rôle.
Débit trop élevé
Le premier consiste à contraindre au débit réservé un flot qui émettrait à
un débit plus élevé. Ce rôle peut être assuré par un lisseur de trafic à
l'entrée de la région sans état. Ce lissage systématique n'a pas d'influence
sur le délai maximal des paquets, car dans le modèle classique le lissage
peut de toute façon potentiellement être réalisé dans n'importe lequel des
noeuds (au premier noeud congestionné, le flot ne pourra pas utiliser
plus que la bande passante réservée et sera donc lissé au débit
correspondant). Évidemment, il est probable que le délai moyen soit augmenté
mais cela ne nous semble pas être un problème. Le corollaire est d'ailleurs
une diminution de la gigue au récepteur.
De plus, le flot étant lissé à l'entrée de la zone sans état, aucun tampon
autre que ceux nécessaires à l'arbitrage de la contention (donc de taille
réduite) n'est requis à l'intérieur de la zone. Celle-ci étant typiquement
un réseau à haut débit devant utiliser des mémoires très rapides et donc
coûteuses, cela permettra des économies substantielles. Cette économie se
reflète également en gestion puiqu'il n'est plus nécessaire de réserver et
gérer l'occupation de tampons par flot. Il suffira au contraire de
les dimensionner suffisamment pour ne pas risquer de pertes dues à la
contention.
Changement de la taille de paquet
Il s'agit à notre avis d'un problème secondaire. On peut simplement se
ramener au cas d'une taille de paquet constante en ``bourrant'' les paquets
trop courts au niveau de l'ingress, de façon à n'avoir que des paquets de
taille Li constante pour chaque flot i dans la zone sans état. Il faut
alors faire l'opération inverse à la sortie. On peut néanmoins agir plus
subtilement, c'est à dire faire simplement en sorte que les paquets soit
traités comme s'ils avaient une taille Li fixée. Par exemple, au lieu de
transporter la valeur de Ri dans le paquet, on peut transporter
directement Li/Ri (la valeur de Ri n'étant utilisée dans le calcul de
l'estampille que comme diviseur de Li).
Il faut cependant bien noter que dans ce cas une application ne peut pas
supposer qu'elle obtiendra des délais plus faibles si à un moment donné elle
réduit la taille de ses paquets.
Correction de la gigue
Une solution déterministe a été apportée à cet aspect dans
[SZ99]. Brièvement, l'idée est d'utiliser une variante de
Virtual Clock qui contrôle la gigue (c'est une discipline qui ne
conserve pas le travail). Au moment où un paquet est émis, la différence
entre les instants de départ effectif et théorique est placée dans un champ
de l'en-tête du paquet. Au noeud suivant, cette valeur sera utilisée pour
retarder le paquet. Ainsi la gigue ne peut s'ajouter de noeud en noeud,
elle est limitée à L/R.
Nous discutons plus en détail cette solution pour la comparer avec notre
proposition en section 5.6 page ??.
Plutôt que d'assurer un contrôle strict de la gigue, nous prenons comme
optique de prévoir et prendre en compte les effets de la gigue sur les
garanties.
5.4.4 Les effets de la gigue
Si la gigue créée par le noeud précédent n'est pas corrigée par le terme
Fik-1, l'estampille du paquet Pik arrivé ``en avance'' va être
plus petite que ce qu'elle devrait être pour émuler correctement le
TDM. Cela se traduira éventuellement par un gain de placement pour la
résolution de la contention au détriment des paquets d'autres flots en
contention. L'ordonnanceur n'émule plus correctement le modèle de référence
puisqu'il alloue à cet instant au flot i plus de bande passante que ce qui
lui est dû. Il émule alors un serveur fluide qui servirait deux paquets du
flot i simultanément. Par exemple, sur la figure 5.2 le
paquet 2 arrive en avance, un ordonnanceur VC classique repousse son
estampille pour émuler correctement le TDM alors qu'un ordonnanceur qui ne
connaît pas la valeur de Fi1 (appelons le stateless VC) commet
une erreur sur le calcul de Fi2. Cette sur-consommation des ressources
par le flot n'a pas d'effet sur le flot lui même (à part une augmentation de
la gigue) mais peut par contre résulter en une violation des garanties dûes
aux autres flots.
Figure 5.2 : Service de deux paquets du même flot en parallèle
Plus grave, les effets de la gigue peuvent s'accumuler lors des traversées
de noeuds successifs. Si dans le pire des cas, on peut comme nous l'avons
montré obtenir un grumeau de deux paquets complètement collés après un noeud, la taille de grumeau maximum théorique après n noeuds sera de n+1
paquets collés (figure 5.3). Évidemment, il s'agit d'un cas que
nous qualifierons de pire car hautement improbable mais qu'il n'est
pas possible d'exclure formellement.
Figure 5.3 : Accumulation d'un grumeau
Influence de la charge
Ce phénomène d'agglomération dépend essentiellement de la charge. Soit l
la charge instantanée à un moment donné sur un noeud. Le délai maximal
subi par un paquet et correspondant au délai de paquetisation dans le modèle
fluide est égal à l × L/R. Cela s'explique par le fait que
dans l'ordonnanceur discret, ce délai correspond à la résolution de la
contention entre les paquets. Ainsi, quand la charge à un instant donnée est
maximale, il faut au maximum un temps égal à L/R pour ``écouler'' tout le
trafic. Si la charge est réduite de x %, moins de paquets sont en
contention, le temps nécessaire pour écouler toutes les données est lui
aussi réduit de x %.
Cependant, la charge instantanée maximale possible sur un noeud croit avec
la déformation du trafic. Des grumeaux de taille plus élevée signifient une
charge instantanée potentielle plus élevée. Ainsi, la charge influe sur la
déformation du trafic, et la déformation du trafic induit une charge
maximale plus importante au noeud suivant. La déformation sera alors plus
importante, etc...
Acceptabilité de la gigue
À nouveau la charge
Appelons charge statique le rapport de la somme des réservations
allouées sur la capacité du lien :
Si ls est inférieure à un, le réseau est en fait sous
provisionné. Ainsi, un flot i auquel est réservée une bande passante
Ri peut en fait consommer une bande passante jusqu'à Ri/ls
(puisque åj
Rj/ls = C).
Dans une telle situation, une surcharge pour chaque flot (c'est à dire des
grumeaux) est acceptable sans risquer de violer aucune des garanties faites
aux autres flots. Pour prendre un exemple très simple, une charge de 50 %
signifie que deux fois plus de bande passante que ce qui a été réservé est
disponible instantanément. Des grumeaux de taille deux n'auront alors aucun
effet sur les garanties ; dans le cas pire où un grumeau de taille
deux pour chaque flot arrivent en même temps sur l'ordonnanceur, l'ensemble
de la bande passante disponible est consommée à cet instant sans qu'aucun
flot ne reçoive moins de bande passante que ce qui lui avait été réservé.
Cas des flots à faible débit
Pour les flots qui utilisent moins que leur débit réservé (flots à faible
débit demandant un délai faible par exemple), les effets de l'agglomération
sont retardés. Si le flot a un débit r et une réservation R,
l'incertitude sur l'instant d'émission est égale à L/R < L/r.
Il s'agit en fait du même phénomène que nous venons de décrire avec la
charge, mais agissant au niveau d'un flot et non pas globalement. Le flot
disposant de plus de ressources qu'il n'en consomme, il dispose d'une
certaine ``marge'' de déformation acceptable avant de sur-consommer des
ressources, éventuellement au détriment d'autres flots.
Influence globale de la charge
En limitant la charge, nous limitons la proportion de la capacité du lien
allouée aux flots GS. Le trafic best-effort (ou d'une autre classe de
service moins exigeante) traité à une priorité plus faible (c'est à dire
uniquement quand aucun des flots GS n'utilise les ressources) n'entre pas en
compte dans cette charge. On peut donc obtenir les effets d'une charge
réduite sans pour autant limiter l'utilisation du réseau, mais en limitant
la charge statique (c'est à dire la somme de la bande passante réservée
divisée par la bande passante du lien) en flots GS.
Ainsi, si l'on limite la charge statique en flots GS à 50 % de la capacité
du réseau, on réduit le rythme de création des grumeaux tout en rendant
possible le traitement de grumeaux de taille deux paquets sans risquer
aucune violation des garanties.
Au premier noeud, les flots ayant été lissés à l'entrée de la zone sans
état, nous considérerons qu'il n'y a aucun grumeau. La charge instantanée
l1 est alors limitée par la charge statique ls. Une déformation du
trafic est introduite, et dans le pire des cas des grumeaux de taille 2 sont
créés. Ainsi, pour le prochain noeud la charge instantanée potentielle est
doublée. L'intervalle d'incertitude sur le moment d'émission des paquets au
prochain noeud double donc, et des grumeaux de quatre paquets peuvent
apparaître, qui doublent la charge au noeud suivant et ainsi de suite. En
fin de compte, la charge instantanée maximale après n noeuds est :
ln = 2n × ls
Et l'on veut assurer que la charge instantanée ne dépasse jamais la charge
maximale acceptable pour chaque flot compte tenu du sous provisionnement du
réseau, soit :
Donc :
| 2n × ls £ |
|
ÜÞ
2n £ |
|
ÜÞ
n £ log2 |
|
ce qui est représenté sur la figure 5.4.
Figure 5.4 : Longueur maximum en fonction de la charge
On voit très bien qu'une faible réduction de la charge a très peu d'effet ;
par contre des limitations plus importantes changent significativement la
situation : jusqu'à cinq noeuds peuvent être traversés avec une charge
proche de 20 %. Ce résultat n'est cependant valable que si la déformation
des flots rencontrés dans les noeuds augmente progressivement le long du
chemin, ce qui dépend de la topologie du réseau.
Nous insistons sur le fait que ce résultat correspond à une situation
pire et hautement improbable. En pratique, on devrait donc
obtenir des comportements bien meilleurs.
Nous appelons stateless VC la discipline de service inspirée de
Virtual clock et ne maintenant pas l'état Fik-1. Elle utilise
le calcul suivant pour le calcul de l'estampille d'un paquet :
Évidemment, deux situations sont possibles, dans lesquelles l'algorithme
émule correctement ou non le TDM.
| (1) |
Aik ³ Fik-1 |
correct |
| (2) |
Aik < Fik-1 |
erreur |
Dans le cas (1), le paquet arrive après le Fi du paquet précédent, Aik
> Fik-1 et donc le fonctionnement est identique à la version avec
états.
Dans le cas (2), le paquet arrive avant le Fi du paquet précédent. Il y a
donc là erreur et mauvaise émulation du TDM. Néanmoins, si certaines
précautions sont prises, cette erreur devrait se produire assez peu et
surtout ses conséquences peuvent être contrôlées.
5.4.5 Suppression partielle du terme Fik-1
Nous venons de voir qu'il est possible dans certaines conditions de ne pas
contrôler à chaque noeud la gigue prise par les paquets. Cependant on peut
aussi dans une certaine mesure contrôler cette gigue sans pour autant créer
un état dédié. L'idée est d'utiliser l'information déjà présente dans la
file de paquets en attente.
Rappelons que les paquets en contention sont triés sur leur estampille
Fik dans une file d'attente. Ils doivent être stockés avec leur
estampille pour conserver une file triée lors de l'insertion de nouveaux
paquets. Ainsi quand un paquet arrive, si on sait qu'un paquet du même flot
est en attente, on connaît la valeur à utiliser pour le
Fik-1. Évidemment, le fait qu'aucun paquet du même flot ne soit
présent dans la file n'assure pas que l'on ait Aik ³
Fik-1. fik étant la date de départ effectif du kieme
paquet du flot i, le calcul à appliquer est alors :
|
|
ì
ï
ï
í
ï
ï
î |
|
si |
Aik ³ fik-1 |
|
si |
Aik < fik-1 |
|
|
(5.3) |
Trois situations sont possibles :
| (1) |
Aik ³ Fik-1 |
correct |
| (2) |
Aik £ fik-1 £ Fik-1 |
correct |
| (3) |
Aik < Fik-1 £ fik-1 |
erreur |
Dans le cas (1), le paquet arrive après le Fi du paquet précédent, Aik
> Fik-1 et donc le fonctionnement est identique à la version avec
états.
Dans le cas (2), le paquet arrive avant le Fi du paquet précédent et
avant le départ effectif de ce paquet. La valeur Fik-1 est
récupérée et le fonctionnement est identique à la version avec états.
Dans le cas (3), le paquet arrive avant le Fi du paquet précédent et
après le départ effectif de ce paquet. La valeur Fik-1 n'est
plus disponible et l'algorithme suppose que l'on se trouve dans le cas
(1). Il y a donc là erreur et mauvaise émulation du TDM.
L'utilisation de cet algorithme suppose deux choses :
-
que l'on puisse identifier un flot,
- que l'on puisse retrouver un paquet d'un flot donné (s'il existe) dans
la file.
L'identification d'un flot peut se faire de manière classique (paire
d'adresses et ports source/destination) ou en utilisant un label attribué
par le routeur ingress, ce qui permettrait un traitement plus simple. Ce
label pourrait par exemple être constitué d'un identificateur de l'ingress
et d'un numéro de flot unique pour cet ingress. Une liste des estampilles
des derniers paquets de chaque flot présents dans la file peut être
conservée dans une table hachée utilisant l'identificateur de flot comme
clé. Ces opérations demandent un traitement supplémentaire par paquet. Leur
complexité ne dépend pas du nombre total de flots mais du nombre de flots
dont au moins un paquet est présent dans la file qui devrait être beaucoup
plus faible à tout instant.
Nous obtenons une discipline de service située entre le statefull VC
et le stateless VC, que nous appellerons reduced state VC
puisqu'elle n'utilise qu'une quantité réduite d'état déjà disponible. La
motivation derrière cette proposition est que cela devrait être efficace en
cas de grumeaux sévères, donc limiter les effets dans les cas les plus
graves. Ainsi, si des violations de garanties ont lieu du fait d'une gigue
excessive, c'est qu'il y a une augmentation significative de la
contention. Intuitivement, il est clair que dans cette situation la
probabilité du cas (2) augmente alors que celle du cas (3) diminue.
5.4.6 L'architecture proposée
Comme au chapitre 4, nous considérons un ensemble de réseaux dans
lesquels le modèle IntServ/RSVP est déployé, interconnectés par un backbone
utilisant des ordonnanceurs sans état par flot. Nous nous intéressons
uniquement au cas des flots GS, les flots CL étant par exemple traités par
des mécanismes du type SRP [FALB98]. Les flots GS sont donc lissés à leur
débit réservé R à l'entrée du backbone, par les noeuds
ingress qui placent également la valeur de R dans un champ de
l'en-tête du paquet. L'opération inverse est réalisée à la sortie par le
routeur egress (figure 5.5). Un contrôle d'admission
par flot est réalisé de façon à limiter la charge en flots GS à une valeur
fixée, par exemple 80 % de la capacité sur chaque lien.
Figure 5.5 : Architecture de la solution
Dans les noeuds internes, tous les flots autres que GS sont traités en
priorité inférieure (plusieurs niveaux de priorité ou tout autre mécanisme
peuvent être utilisés, par exemple pour séparer trafic best-effort et
flots CL).
| |
Statefull VC |
Reduced state VC |
Stateless VC |
| 1 |
Ri ¬ état du flot |
Ri ¬ paquet |
Ri ¬ paquet |
| |
Fik-1 ¬ état du flot |
Fik-1 ¬ file si Aik < fik-1 |
|
| 2 |
Fik = max(Aik, Fik-1) + Lik/Ri |
Fik = Aik+Lik/Ri si Aik ³ fik-1 |
Fik = Aik + Lik/Ri |
| |
|
Fik = Fik-1 + Lik/Ri si Aik < fik-1 |
|
| 3 |
insertion du paquet dans la file |
| 4 |
état du flot ¬ Fik |
|
|
Table 5.2 : Les trois algorithmes VC
Nous résumons les différences des deux variantes scalable de
l'algorithme virtual clock avec la version complète
(statefull) dans le tableau 5.2.
5.5 Simulations
Le scénario de nos simulations est représenté sur la figure
5.6. Nous considérons un ensemble de flots de référence (sur
lesquels nous effectuerons des mesures) traversant un certain nombre de noeuds dans un backbone et demandant des garanties de délai. L'ordonnanceur
utilisé dans les noeuds est une des trois variantes
stateful/stateless/reduced state VC. À chaque noeud, des flots
parasites viennent partager la bande passante du lien aval avec les
flots de référence. Ces flots parasites sont supposés avoir déjà traversé un
certain nombre de noeuds implémentant le stateless/reduced state VC
et présentent donc des grumeaux susceptibles de perturber le service dû aux
flots de référence.
Tous les flots (sauf un de référence et un parasite à chaque noeud) sont à
débit constant (on suppose qu'ils ont été lissés à l'entrée du backbone) et
ont des ressources réservées dans les ordonnanceurs. Les flots restant (un
flot de référence et un parasite à chaque noeud) sont des flots
best-effort et émettent à un débit élevé, déterminé de façon à
toujours obtenir une utilisation maximale du réseau.
Dans nos simulations, nous faisons varier le nombre de noeuds --
nbcore --, les caractéristiques des flots parasites (taille --
grum -- et type des grumeaux) et la charge en flots
demandant des garanties de délai. Plus exactement, c'est la capacité des
liens que nous faisons varier.
Figure 5.6 : Topologie simulée
Pour chaque valeur des paramètres, nous comparons les résultats obtenus avec
les trois variantes de l'ordonnanceur. Pour toutes les simulations il y a 10
flots parasites à chaque noeud et 10 flots de référence. Nous avons choisi
un nombre réduit de flots pour des raisons pratiques de mise en place et de
temps de simulation. Cela n'est pas un problème dans la mesure où nous ne
cherchons pas à montrer la scalabilité de notre solution (elle l'est car
elle ne nécessite pas la gestion d'états par flot), mais plutôt à évaluer la
qualité du service fourni par rapport à un modèle utilisant des états par
flot.
Tous les flots ont une taille de paquet identique et égale à 1000 octets,
sauf un des flots de référence qui émet des paquets de 500 octets (ce qui
implique une garantie de délai plus faible). Nous effectuerons les mesures
sur deux des flots de référence, le flot 1 (paquets de 1000 octets) et le
flot 3 (paquets de 500 octets).
5.5.2 Réalisation
Nous utilisons le simulateur ns-2 [FVE99] développé au
Lawrence Berkeley National Laboratory de l'Université de Californie à
Berkeley. Celui-ci n'offre pas d'ordonnanceur Virtual Clock en
standard, mais une implémentation en a été réalisée pour une ancienne
version de ns par Markus A. Wischy à l'Université de l'Orégon
[Wis98]. Nous avons porté cette implémentation sur la dernière version
de ns et l'avons modifée de façon à obtenir un comportement soit en
VC classique soit l'une de nos deux variantes sans état.
Il nous fallait ensuite générer du trafic présentant des grumeaux de façon
paramétrable pour les flots parasites. Nous avons utilisé deux méthodes.
Pour la première, nous avons modifié le générateur de trafic à débit
constant de ns (Application/Traffic/CBR) pour obtenir de
grandes variations du temps inter paquets. Ainsi modifiée la source CBR
génère aléatoirement des grumeaux de taille variable. Le trafic obtenu est
ensuite conditionné par un régulateur utilisant un seau de jetons
(token bucket filter, TBF) de façon à limiter la taille
maximum de grumeaux à la valeur désirée.
Nous avons aussi voulu observer le comportement du système dans le cas
pire, c'est à dire avec des flots parasites exhibant systématiquement
des grumeaux de taille fixée. Pour cela, un altérateur de trafic
Clumper a été défini pour modifier le trafic généré par les
sources CBR. Son fonctionnement est très simple, il retient simplement les
paquets qu'il reçoit dans une file d'attente jusqu'à ce que la file atteigne
une taille configurée, il émet alors tous les paquets en attente dans la
file.
Nous appellerons les grumeaux générés de cette façon des grumeaux
lourds (car très sévères) et ceux générés avec la première méthode des
grumeaux légers. Ceux-ci correspondent à des situations plus
réalistes, alors que les grumeaux lourds peuvent nous fournir des
indications sur le comportement de l'algorithme en situation extrême et donc
nous aider à comprendre son fonctionnement. Les caractéristiques de ces deux
types de trafics parasites sont décrits dans la section suivante.
5.5.3 Caractérisation des flots parasites
Nous proposons d'utiliser comme méthode de caractérisation d'un flot
parasite la représentation graphique de la distribution des temps
inter paquets de ce flot. Pour cela nous prenons un groupe de deux cents
paquets consécutifs du flot, calculons les temps inter paquets que nous
trions et divisons par le temps nominal afin de normaliser les valeurs. Nous
traçons la courbe obtenue.
Ainsi, un flot à débit constant parfait aura une caractérisation
correspondant à une ligne horizontale d'ordonnée un (équation y=1). La
figure 5.7 montre les courbes obtenues dans le cas des
grumeaux légers pour différentes configurations du régulateur.
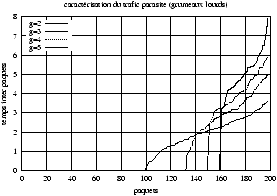
Figure 5.7 : Caractérisation du trafic parasite (grumeaux légers)
Si aucun seau de jetons ne conditionne le trafic généré par la source CBR
modifiée, le temps inter paquets est réparti uniformément entre 0 secondes
et deux fois le temps nominal. On obtient donc un segment de droite variant
entre y=0 et y=2. Quand un seau de jetons vient limiter la taille de
rafale (donc la taille des grumeaux), une partie des paquets est contrainte
au débit nominal (lissage) ce qui apparaît graphiquement comme un segment de
droite central sur (y=1), dont la longueur est inversement liée à la
profondeur du seau de jetons utilisé.

(a) source CBR ``pure''
(b) source CBR modifiée
Figure 5.8 : Caractérisation du trafic parasite (grumeaux lourds)
La figure 5.8 montre les caractérisations obtenues pour les
grumeaux lourds. La sous figure 5.8(a) représente le cas où
le clumper est appliqué au trafic issu d'une source CBR parfaite. On
voit, ce qui correspond tout à fait à l'intuition, que si les grumeaux
formés sont de taille 2, la moitié des paquets a un temps inter paquets nul,
et l'autre moitié un temps double de la normale. Le même raisonnement
s'applique pour toutes les tailles de grumeaux.
La sous figure de droite 5.8(b) correspond au cas où le
clumper est appliqué au trafic issu d'une source CBR modifiée,
dont la répartition des temps inter paquets est uniforme dans l'intervalle
compris entre zéro et deux fois le temps nominal. C'est le cas que nous
avons utilisé dans nos simulations.
Dans tous les cas, il nous paraît clair que l'effet du trafic parasite sur
le comportement de l'ordonnanceur sans état dépendra de son
agressivité qui correspond graphiquement à la partie de la courbe
située sous la droite (y=1).
Le but des simulations est de déterminer dans quelles conditions nos deux
variantes du Virtual Clock, stateless VC et reduced
state VC ont un comportement (et fournissent des garanties) identique ou
très proche de celui de l'ordonnanceur de référence, le statefull VC.
Pour chaque configuration de simulation, nous mesurons :
-
les délais maximaux,
- la caractérisation du trafic en sortie, telle que définie en
5.5.3.
Les délais permettront d'évaluer le comportement de l'ordonnanceur tandis
que la caractérisation du trafic permettra de vérifier la validité du modèle
de trafic utilisé pour les flots parasites.
Déviation de délai
Nous ne voulons pas mesurer le délai fourni par chacune des variantes mais
plutôt la différence par rapport au délai de référence. Nous définissons
donc le sur-délai dans un contexte donné comme étant le rapport du
délai fourni par l'ordonnanceur sans ou avec peu d'états sur le délai fourni
par l'ordonnanceur de référence. Toutes les courbes de sur-délai présentées
dans la suite sont celles du flot 1, les courbes sont globalement similaires
pour le flot 3.

(a) Grumeaux légers

(b) Grumeaux lourds
(c) Grumeaux légers -- stateless

(d) Grumeaux légers -- reduced state
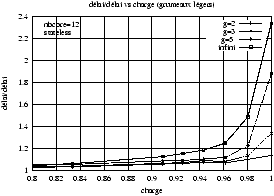
Figure 5.9 : Sur-délai vs charge
Les figures 5.9(a) à (d) montrent le sur-délai de chacune
des deux variantes en fonction de la charge pour les deux types de grumeaux
pour différentes configurations. Dans les figures (a) et (b), le nombre de
noeuds traversés est fixé à 6. La première montre très nettement que le
sur-délai reste très faible tant que la charge est inférieure à 95 %, ce
qui nous paraît un résultat extrêmement positif. Dans la deuxième, l'effet
des grumeaux lourds se fait plus sentir et le sur-délai augmente
progressivement avec la charge. Nous expliquons l'aspect de la courbe du
reduced state VC plus bas, en commentant la figure
5.11. Les figures (a) et (b) correspondant à des tailles de
grumeaux limitées à trois, nous montrons avec les figures (c) et (d)
l'influence de cette limitation. Celle-ci ne devient sensible que quand la
charge approche de très près les 100 %. On note tout particulièrement que
pour le cas pire où les grumeaux ne sont pas contraints (noté ``infini'')
les courbes restent dans le même ordre de grandeur.
Les figures 5.10 et 5.11 montrent le
sur-délai en fonction de la taille des grumeaux des flots parasites pour
différentes valeurs de la charge (le nombre de noeuds traversés est
toujours fixé à 6). On voit sur la figure 5.10 qu'avec une
charge de 100
%, le sur-délai augmente nettement avec la taille des grumeaux. Deux
résultats intéressants sont visibles sur cette figure. Premièrement, avec
une charge maximale, l'ordonnanceur reduced state VC se comporte
nettement mieux que le stateless VC, ce qui s'explique par le fait
que la charge maximale résulte en une contention assez forte et que la
situation (2) (décrite page ??) est assez
fréquente. Deuxièmement, l'effet d'une réduction même minime de la charge
est très important comme le montre la courbe correspondant à une charge de
98 %. Si la charge est réduite à 90
%, le sur-délai est extrêmement faible (moins de 5 et 7 % de délai ajouté)
quelle que soit la taille des grumeaux. La différence entre les deux
variantes est alors très légère mais visible.
Figure 5.10 : Sur-délai vs taille des grumeaux
La figure 5.11 montre les mêmes courbes dans le cas de
grumeaux lourds. Nous constatons que l'impact des grumeaux est beaucoup plus
important et que l'effet d'une diminution de charge est nettement moins
visible.
Figure 5.11 : Sur-délai vs taille des grumeaux
Le reduced state VC fournit alors exactement le même délai que la
référence. Cela s'explique par le fait que les paquets collés dans les
grumeaux lourds créent systématiquement la situation (2).
La troisième paire de figures montre le sur-délai en fonction du nombre de
noeuds traversés sous diverses charges. Dans le cas de grumeaux légers
(figure 5.12), on retrouve à nouveau des sur-délais très
faibles tant que la charge ne dépasse pas 90 % et un avantage significatif
du reduced state VC quand la charge approche 100 %, toujours pour
les mêmes raisons. L'effet d'une très légère diminution de charge est à
nouveau très net. On constate également que le sur-délai est globalement
indépendant du nombre de noeuds, c'est à dire que le délai absolu ajouté
augmente proportionnellement au nombre de noeuds traversés. La figure
5.13 montre les mêmes résultats pour des grumeaux
légers non contraints, avec simplement des valeurs de surdélai un peu plus
élevées.
Dans le cas de grumeaux lourds (figure 5.14), on voit à
nouveau que le reduced state VC devient équivalent à un
statefull VC. Avec le stateless VC, le sur-délai reste
significatif tant que la charge ne descend pas au dessous de 70 %.
Figure 5.12 : Sur-délai vs nbre de noeuds (grumeaux légers)
Figure 5.13 : Sur-délai vs nbre de noeuds (grumeaux légers) -- cas pire
Figure 5.14 : Sur-délai vs nbre de noeuds (grumeaux lourds)
Caractérisation du trafic en sortie
Nous comparons maintenant la caractérisation des flots de référence en
sortie du réseau avec celle des flots parasites dans le cas des grumeaux
légers. Nous considérons que les résultats des simulations sont valables
quand les flots de référence en sortie du réseau ne sont pas plus agressifs
que les flots parasites.
Figure 5.15 : Caractérisation du flot 1
Une première remarque que l'on peut faire à partir des figures
5.15 et 5.16 est que les caractérisations
des flots de référence en sortie et des flots parasites ont une allure assez
proche, bien qu'un peu différente, les flots de référence montrant une
caractérisation plus ``lisse''. Il ne sera donc pas toujours possible de
juger de manière catégorique de l'agressivité comparée des deux
caractérisations.
La figure 5.15 montre le cas du flot 1. On constate que dans
tous les cas, et à charge maximale, le flot est assez peu agressif puisque
le temps inter paquets minimal ne descend pas au dessous de la moitié du
temps nominal. On voit très bien qu'il est nettement moins agressif qu'un
flot parasite contraint à une taille de grumeaux de trois. On peut donc
considérer que les résultats obtenus avec des grumeaux de taille trois ou
supérieure sont valables. La comparaison avec la courbe parasite pour des
grumeaux de taille deux est plus difficile.

(a) Charge de 100 %

(b) Charge de 94 %
Figure 5.16 : Caractérisation du flot 3
La figure 5.16 montre le cas du flot 3. L'impact que la
traversée du réseau a eu sur sa caractérisation est nettement plus élevé que
pour le flot 1 (le temps inter paquets minimal approche la valeur 0), ce que
nous attribuons au fait que ses paquets sont de taille nettement inférieure
(moitié) à celle des flots parasites. L'aspect plus ``saccadé'' peut
s'expliquer de la même façon.
La figure 5.16(b) montre l'influence d'une diminution de la
charge sur la caractérisation du flot 3. Avec une charge de 94 %, les flots
parasites n'étant pas contraints, le flot est très clairement moins agressif
qu'un trafic parasite avec des grumeaux de taille 3.
Ainsi, les résultats obtenus en terme de délai semblent être valables dans
pratiquement n'importe quelles conditions si les tailles de paquets des
flots parasites et de référence sont identiques. Dans le cas de tailles de
paquets différentes, on obtient des résultats similaires avec une légère
diminution de la charge.
Délais absolus
Il nous paraît intéressant de montrer que même dans les cas où
l'ordonnanceur sans état fournit un délai sensiblement plus important que
l'ordonnanceur de référence, cela n'entraîne pas forcément une violation des
délais garantis aux flots.
(a) Statefull VC

(b) Stateless VC
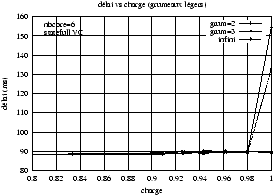
Figure 5.17 : Délais absolus
Ainsi, la figure 5.17 montre les délais en fonction de la
charge obtenus avec les ordonnanceurs statefull et stateless VC. Le délai
garanti de manière déterministe est de 175 ms, et l'on constate que la
plupart du temps les délais maximaux effectifs sont bien inférieurs, ce qui
est un résultat connu.
Conclusion
Les résultats de nos simulations montrent que notre solution semble
fonctionner correctement dès que l'on réduit légèrement la charge en flots à
garanties de délai. Même avec des tailles de grumeaux élevées, le délai
ajouté par rapport au modèle de référence est très faible dès que la charge
ne dépasse pas 90 % pour des grumeaux légers, les plus réalistes.
On peut aussi prendre en compte le fait que le modèle de référence fournit
toujours des délais nettement moins élevés que ceux qui sont garantis comme
montré dans les courbes de la figure 5.17. Il peut donc être
parfois tout à fait acceptable d'obtenir un sur-délai significatif.
La contrainte de devoir limiter la proportion de flots à garantie de délais
ne nous semble pas gênante. La plupart des applications peuvent se
satisfaire de garanties moins strictes et constitueront donc une part
significative du trafic transporté par le réseau.
Enfin, même dans le cas d'un réseau qui ne transporterait que ce type de
flots, le sur-dimensionnement nécessaire pour limiter la charge pourrait
être très raisonnable. Ainsi, la figure 5.9(a) montre des
courbes pratiquement plates jusqu'à 90 % de charge.
5.6 Comparaison avec DPS
Dans [SZ99], Stoica et Zhang obtiennent des délais
déterministes en utilisant la technique DPS (Dynamic Packet
State) ce qui rend leur solution supérieure à la notre sur le plan
théorique. Cependant, la technique qu'ils utilisent pour obtenir ce résultat
est beaucoup plus complexe et nécessite un supplément de traitement par
paquet important.
Ils proposent d'utiliser un ordonnanceur CJVC (Core Jitter Virtual
Clock). Il s'agit d'une version sans état de Jitter Virtual Clock,
une variante non work-conserving de VC qui conserve la gigue entre
les paquets. Comme il est impossible de réduire les variations sur le moment
d'émission d'un paquet dans un noeud (L/R+Lmax/C), l'écart entre le
moment effectif (fik) et le moment théorique d'émission (Fik) est
stocké dans le paquet au moment de l'émission. Cette valeur qui représente
``l'avance'' prise par le paquet dans ce noeud est ajoutée dans le calcul
du Fik au noeud suivant. La gigue est ainsi compensée à chaque noeud.
Le fait d'utiliser un algorithme qui conserve la gigue leur permet aussi de
traiter le cas des paquets de tailles différentes. Il suffit pour cela de
compenser l'avance éventuelle prise par un paquet sur son prédécesseur en
ajoutant à chaque noeud un délai adéquat. Ce délai est calculé par le noeud ingress qui le place dans un champ d'en-tête du paquet.
Au niveau du plan de contrôle, ils proposent de n'utiliser des messages (non
fiables) que pour ajouter des réservations, l'annulation étant prise en
compte par une technique de mesure du débit réservée semblable à notre
proposition, mais nettement plus complexe.
Notre solution est résolument plus simple et légère. Nous utilisons un
ordonnanceur qui conserve le travail, simple à implémenter. Aucune
modification particulière du contenu des champs d'en-tête des paquets n'est
nécessaire à l'intérieur de la zone sans état. Enfin nous n'avons besoin que
d'un champ d'en-tête pour stocker la valeur de Ri.
En conclusion, notre proposition est plus simple à implémenter, demande
moins de puissance de traitement et nécessite moins de supplément d'en-tête
dans les paquets. Par contre, les garanties ne sont pas assurées de manière
déterministe. Notre approche est plus basée sur des hypothèses raisonnables
et vérifiables en pratique sur la déformation du trafic (création de
grumeaux) et son effet sur les garanties.
5.7 Conclusion du chapitre
Dans ce chapitre, nous avons proposé une architecture permettant de fournir
des garanties de délai individuelles aux flots (avec donc une flexibilité
maximale) sans nécessiter le maintien d'état pour chaque flot. Les
contraintes de cette solution sont de lisser les flots à l'entrée du
backbone et de limiter (de façon peu drastique) la capacité
allouée aux flots demandant des garanties de délai.
Les outils analytiques ne pouvant nous donner que des résultats non
significatifs, nous avons eu recours à la simulation pour obtenir des
données plus utilisables. L'utilisation réelle de ce modèle nécessiterait
sans doute une analyse plus poussée des phénomènes entrant en jeu, en
particulier :
-
caractériser la création des grumeaux dans des situations réalistes,
- caractériser l'effet cumulé des grumeaux au long d'un chemin (en
particulier l'influence de tailles de paquets différentes).
De plus, dans le cas de la variante reduced state VC de
l'ordonnanceur, il serait nécessaire d'évaluer la complexité liée à la
gestion des états, et en particulier la taille maximale de la file de
paquets.
Nous pensons néanmoins que nos simulations ont montré, comme c'était leur
but, que l'approche était utilisable dans des conditions bien moins
drastiques que celles données par les résultats théoriques. Elle peut donc
être présentée comme une solution possible pour la fourniture de garanties
de délai strictes dans des environnements à très grand nombre de flots.
- 1
- Sous réserve que tous les flots
aient émis au moins un paquet. Cela sera généralement le cas si l'intervalle
de temps choisi est suffisament grand. Les routeurs de bordure (voir la
section 5.4.6) peuvent éventuellement émettre un paquet pour les
flots silencieux.
- 2
- Le
retard n'est pas nécessairement effectif puisqu'il s'agit d'une estampille
destinée à arbitrer la contention.
- 3
- Nous considérons qu'un paquet a été
transmis/reçu quand son dernier bit a été transmis/reçu.